梯度下降算法
梯度下降算法是一个用来求函数最小值的算法,我们将使用梯度下降算法来求出代价函数的最小值。
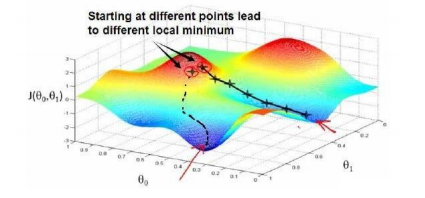
我们想要使用梯度下降来找到最优的:首先随机选择两个(例如,),不断地改变它们的值使得变小,最终找到的最小值点。此时我们得到的最小值为局部最小值,梯度下降算法受初始状态的影响,所以不能确定我们得到的局部最小值是否为全局最小值,选择不同的初始参数组合,可能会找到不同的局部最小值。
批量梯度下降算法公式:
- := -表示赋值
- -学习率,它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。α越小,步长越小,α越大,步长越大
- -梯度
在批量梯度下降中,我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。
在梯度下降算法中,我们要更新和,当和时,会产生更新,所以你需要同时更新和。
实现方法:计算公式右边部分,通过那一部分计算出和的值,然后同时更新和。
梯度和学习速率
对赋值,使得按梯度下降最快的方向进行,一直迭代下去,最终得到局部最小值。是学习率,它决定了我们沿着能让代价函数下降程度最大的方 向向下迈出的步子有多大。
如果太小了,即我的学习速率太小,结果就是只能这样像小宝宝一样一点点地挪动,去努力接近最低点,这样就需要很多步才能到达最低点,所以如果太小的话,可能会很慢,因为它会一点点挪动,它会需要很多步才能到达全局最低点。
如果太大,那么梯度下降法可能会越过最低点,甚至可能无法收敛,下一次迭代又移动了一大步,越过一次,又越过一次,一次次越过最低点,直到你发现实际上离最低点越来越远,所以,如果太大,它会导致无法收敛,甚至发散。
由于随着我们越来越接近最低点,相应的梯度(绝对值)也会逐渐减小,所以每次下降程度就会越来越小,我们并不需要减小的值来减小下降程度。
梯度下降的线性回归
梯度下降算法:
线性回归算法:
在线性回归问题运用梯度下降法,关键在于求出代价函数的导数:
j=0时:
j=1时:
则算法改写成:
批量梯度下降:在梯度下降的每一步中,我们都用到了所有的训练样本,在梯度下降中,在计算微分求导项时,我们需要进行求和运算,所以,在每一个单独的梯度下降中,我们最终都要计算这样一个东西,这个项需要对所有 m 个训练样本求和。
